Thoughts Of Solving Dynamic Programming Problems
Solving the dynamic programming problems
About DP
-
Dynamic programming is a very important algorithm, and mastery of it should be the basic skills for computer science students.
-
Let’s explain as much as possible about the understanding of this type of algorithm.
-
The key is
state definitionandstate transition equation
Longest Increasing Subsequence
Given a sequence of K integers { N1, N2, …, NK }, any contiguous subsequence can be expressed as { Ni, Ni+1, …, Nj }, where 1 <= i <= j < = K. The largest contiguous subsequence is the element and the largest one of all consecutive subsequences, such as the given sequence { -2, 11, -4, 13, -5, -2 }, whose largest contiguous subsequence is { 11, -4, 13 } and the maximum sum is 20.
-
Define
sum[i]as themaximum value of contiguous subsequence with A[i] as the last end -
The state transition equation is:
sum[i]=max(sum[i-1]+a[i], a[i]) -
T he actual solution is, as long as sum>0, then adding a[i] is still possible to increase max; but if sum<0, it should be discarded immediately, starting from 0 to calculate the next
“starthighlight” a = {4, 8, -12, 3, 7, 9} n = len(a) sum = 0 max = 0 for i in range(n): sum += a[i] if sum > max: max = sum if sum < 0: sum = a[i] return sum “endhighlight”
{% highlight Java %}
public int LIS(int[] arr) { int i, j, max = 0; int n = arr.length; int[] list = new int[n]; // length Arrays.fill(list, 1); int[] index = new int[n]; // distance Arrays.fill(index, -1);
for (i = 1; i < n; i++)
for (j = 0; j < i; j++) {
if (arr[i] > arr[j] && list[i] < list[j] + 1) {
list[i] = list[j] + 1;
index[i] = j;
}
}
// choose the max
int max_index = 0;
for (i = 0; i < n; i++)
if (list[i] > max) {
max = list[i];
max_index = i;
}
StringBuilder builder = new StringBuilder();
builder.insert(0, arr[max_index]);
int next_index = index[max_index];
while (next_index != -1) {
builder.insert(0, arr[next_index] + " ");
next_index = index[next_index];
}
System.out.println(builder.toString()); // print the result
return max;
“endhighlight”
Number tower problem
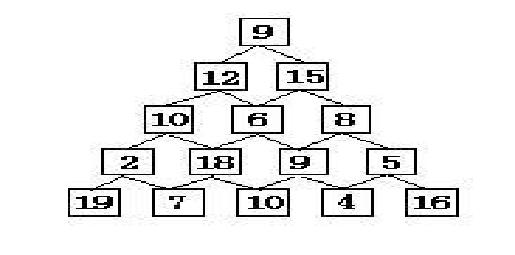
From the top layer to the bottom layer, each layer can only go to the adjacent node, and calculate the sum of the numbers
-
Define the state equation:
max[i,j]represents the sum of the largest numbers passed by [i,j] as the starting point. Thenmax[1,1]is our target -
Define the state transition equation:
max[i,j]=num[i,j]+max(max(i+1,j),max(i+1,j+1)) -
Then you can choose to solve it from top to bottom or from bottom to top
{% highlight C %}
#include
#include
using namespace std;
#define maxnum 1000
int num[maxnum][maxnum];
int d[maxnum][maxnum];
int main(void)
{
int i,j,k;
int n,m;
cin»n;
while(n–){
cin»m;
for(i=1;i<=m;i++)
for(j=1;j<=i;j++)
cin»num[i][j];
for(j=1;j<=m;j++) d[m][j]=num[m][j];
for(i=m-1;i>=1;i--)
for(j=1;j<=i;j++)
d[i][j]=num[i][j]+max(d[i+1][j+1],d[i+1][j]);
cout<<d[1][1]<<endl;
memset(d,0,sizeof(d));
}
}
“endhighlight”
Backpack Problem
- There are different versions of backpack problem.Let me illustrate the basic one.
There are N items and a backpack with a capacity of V. The cost of the i-th item is c[i] and the value is w[i]. Decide which items are loaded into the backpack so the sum of the values can be max.
- Solve it with Java.There are two types of answer,see the comment.
{% highlight Java %} public int Knapsack1(int[] value, int[] weight, int capacity, int number) { if (capacity <= 0 || number == 0) return 0; if (weight[number - 1] > capacity) return Knapsack1(value, weight, capacity, number - 1); else return max(value[number - 1] + Knapsack1(value, weight, capacity - weight[number - 1], number - 1), Knapsack1(value, weight, capacity, number - 1));
}
public int Knapsack2(int[] value, int[] weight, int capacity, int index) {
if (capacity <= 0 || index >= value.length)
return 0;
if (weight[index] > capacity)
return Knapsack2(value, weight, capacity, index + 1);
else
return max(value[index] + Knapsack2(value, weight, capacity - weight[index], index + 1),
Knapsack2(value, weight, capacity, index + 1));
}
// two ways to solve it
int[] value = {60, 100, 120};
int[] weight = {10, 20, 30};
int capacity = 50;
int number = value.length;
System.out.println(dp.Knapsack1(value, weight, capacity, number)); // final result is 220
int index = 0;
System.out.println(dp.Knapsack2(value, weight, capacity, index)); // final result is also 220
“endhighlight”
303 Range Sum Quwey - Immutable
-
About the meaning:Give an array that returns the value of any two range of ranges
-
Idea: The rpblem content says
many calls to function, so the traversal solution will definitely be TLE(Time Limit Exceeded); andsum[i,j]=sum[j]-sum[i-1]is obvious, so all the sums are found in one pass. After the value is done, subtraction is fine. Note you may need to use global variables -
code:
{% highlight C %}
// written in c++
// Using vector
int sumRange(int i, int j) {
if (i==0)
return dp[j];
else
return dp[j]-dp[i-1];
}
}; “endhighlight”
Writen in Python:
“starthighlight” class NumArray(object): def init(self, nums):
self.dp = nums
for i in range(1,len(nums)):
self.dp[i] += self.dp[i-1]
def sumRange(self, i, j):
return self.dp[j] - (self.dp[i-1] if i > 0 else 0)
“endhighlight”
70 climbStatirs
-
About the meaning:Ascend a staircase, you can take 1 step or take two steps.if you go to n steps, how many solutions will you have?
-
Idea: Use dp[n] to indicate the number of methods to go to n steps. For dp[n-1], you can only choose to take 1 step; for dp[n-2], If you choose 1+1, it will overlap with dp[n-1], you can only choose 2 steps.
-
Code:
{% highlight C %} Written in C++ class Solution { public: int climbStairs(int n) { int dp[n]={0}; dp[0]=0; dp[1]=1; dp[2]=2; for(int i=3;i<=n;i++) dp[i]=(dp[i-1]+dp[i-2]); return dp[n]; } }; “endhighlight”
“starthighlight”
written in Python
class Solution(object): def init(self): self.dp={}
def climbStairs(self, n):
self.dp[1]=1
self.dp[2]=2
for i in range(3,n+1):
self.dp[i]=self.dp[i-1]+self.dp[i-2]
return self.dp[n]
“endhighlight”
64 Minimum Path Sum
-
About the meaning:
m*nis a matrix of all positive numbers, which can be moved downwards to the right,find the sum of the distances from the upper left to the lower right. -
Idea: Dynamic programming.using dp[i][j] to represent the shortest number of steps taken with i, j as the last square. Then
dp[i][j]=max(dp[i-1][j]+grid[i][j],dp[i][j-1]+gird[i][j],we just need to implement the equation. -
Code:
{% highlight C %}
// written in C++
class Solution {
public:
int minPathSum(vector<vector